OPENING QUESTIONS: Please review your working model with your groupies... where is your model strong, where is it weak?

1) How does charge change through a circuit? (caps, resistors, series, parallel)

2) How does current change through a circuit? (caps, resistors, series, parallel)

3) How does voltage change through a circuit? (caps, resistors, series, parallel)

OBJECTIVE: I will finalize my working model to calculate circuit values during today's class

TERMS:

• Capacitor - two charged surfaces that can store electrical energy
• Resistor - an object in an electric circuit which interferes with the flow of electrons through that circuit.
• Series: occurs when items in a circuit are connected in a line
• Parallel: occurs when items in a circuit
• ElectroMotive Force = EMF= ε=Voltage

UNITS:

• Capacitance = C
  • (SI Units "farads" = f)
• EMF = ε =Voltage generated inside a battery
  • (SI Units = "Voltage or Volts"="V")
• Voltage = ∆V = Voltage available to a circuit
  • (SI Units = "Voltage or Volts"="V")
• Current = I = Current through an electrical circuit
  • (SI Units = "amperes or Amps"="A")
• Ohms = R=resistance =
  • (SI Units = "ohms" = Ω)
• Power = P = I²R
  • (SI Units = "Watts" = W)

FORMULAE:

• ε=IR (ε = ElectroMotive Force) = Total *oomph* inside the battery, it is not generally equal to the voltage output by the battery because of the internal resistance inside the battery
• ∆V = IR = "Ohm's Law": (We'll use this UNLESS EMF is given)
• P = I²R = Power
• The sum of the voltages around ANY loop in a circuit = 0.

════════════════════

Here's an interesting thought -- we frequently 'reduce' an electric circuit to obtain the "equivalent resistance' for that circuit. Why do we do that?

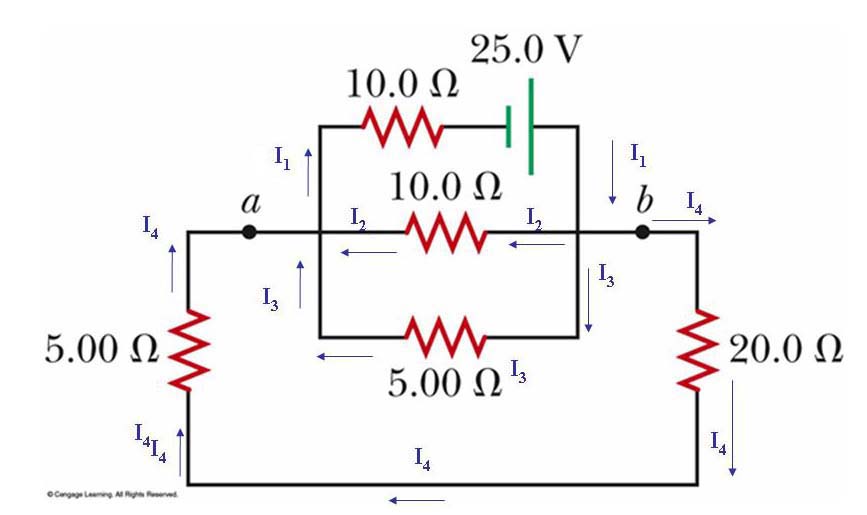
Consider the following diagram:

We can *Reduce* the circuit to a single resistor with an 'equivalent' resistance of 12.94 ohms (I think!.... it's one of your hw probs).

Why is that significant?

How does that impact your model?

We'll try a hands-on-ish activity here to refine our model AND put Kirchoff's Laws to work... (by the way, turn to the person next to you and quoteth Kirchoff's 2)

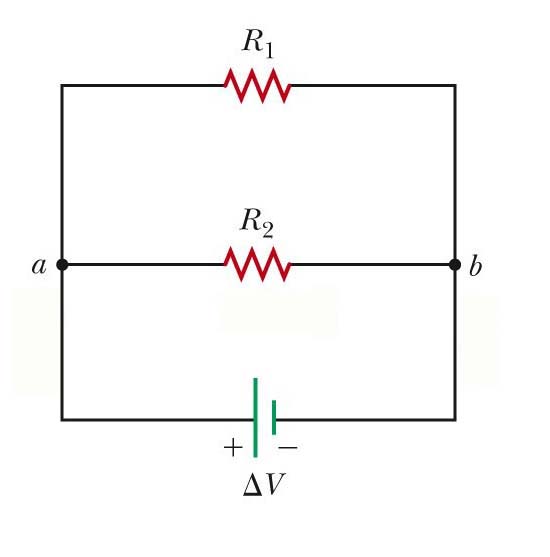
Let's start out with a 24.0 V battery and R₁ = 8.00Ω and R₂ = 12.0Ω :

1) Label all current's with arrows that are kirchoffally appropriate <that should assist with your model>

2) Step 2... why?

3) Step 3... why?